Write a Python program to compute the roots of a quadratic equation. Here's one, let's call it Candice:
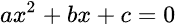
Solve it with this formula. We'll name it Billy:
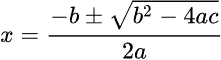
Candice has two solutions. Billy gives both. See that +/- thing? For one solution, it's +. For the other, it's -. So, use Billy twice, once for each solution.

Ray
I don't remember much algebra.
You don't need to. Just get the inputs, and use the formula. You know all you need.
Here's some I/O:
- a? 1
- b? 6
- c? 8
- First solution: -2.0
- Second solution: -4.0
For the square root, put this at the top of your code:
- import math
Then you can compute square roots like this:
- result = math.sqrt(something_goes_here)
Many quadratics don't have real roots, and will crash your program. Here's an example using 1 for a, b, and c:
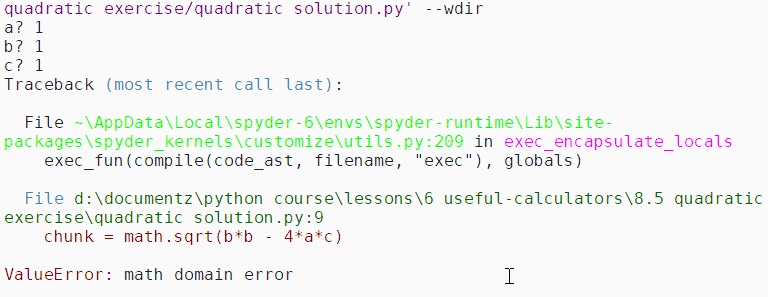
This is normal. Check the formula again, the bit under the square root:
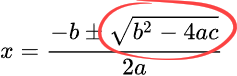
If 4*a*c is more than b*b, you'll get a negative value. For example, when a, b, and c are all 1 (as in the screenshot), b*b - 4*a*c = 1*1 - 4*1*1 = -3.
Trying to find the square root of a negative value is a no-no in standard algebra. It does work when you use complex numbers, where the constant i is the square root of -1, but we're not going there.
Python's standard float type doesn't know what to do with the square root of a negative, and it crashes. That's OK, and expected.
To test your code, use values for a, b, and c that have real solutions. There's a useful page that lets you try different values for a, b, and c. Your program should produce the same results as the program on that page, except when 4*a*c is more than b*b. Here's what that page says when a, b, and c are all 1:

The roots are complex, so the values should crash your program.
However:

Your program should produce the same roots, -4 and -2.
You'll learn a lot about data validation later in the course. You could use what you'll learn to avoid crashy crashy. But let's not worry about it for now.
Include comments for the IPO chunks.
Upload a zip of your project folder. The usual coding standards apply.